This tweet is a great way to introduce optimal transport:
Sinkhorn iteration for Optimal Transport with TF. Code: https://t.co/qn1LXa551F pic.twitter.com/UQgbDlly3g
— Alex Mordvintsev (@zzznah) July 16, 2019
That animation shows interpolation between sets of point clusters that represent various symbols, powered by OT (here’s the IPython notebook that generated the animation, including generating the MP4 video file.
Optimal transport involves transforming one probability distribution (say, images of the letter “A”) into another (say, images of the letter “B”) with minimal cost. It’s the kind of thing we’d code as a Flash demo back in the day with hacks. But in the example above, it’s computed by the very powerful, very general technique of optimal transport.
Diving in
Michiel Stock’s notes on optimal transport are a really good introduction to OT. He explains OT as:
an optimization paradigm where the goal is to transform one probability distribution into another with a minimal cost
When you consider just how broad and general a ‘probability distribution’ is (!), the range of applications are just staggering.
Several ‘cool’ applications immediately leap to mind:
- interpolating along clusters of images a la GANs - along male-female, young-old, etc. dimensions
- color transfer: matching the palette of a source image to the palette of a target image, while keeping the same overall visuals
But there are also mundane and very practical uses too
- as a distance metric between ‘objects’ / probability distributions
- optimizing conflicting complex preferences - allocation of limited food for a group (given some additional constraints / cost function), voting ballot optimization, etc.
- interpolating between sets of N-dimensional point clusters
The lists above barely scratch the surface of what’s possible with OT. Heck, the casual definition of OT (given above) is so general that the hard part is just coming up with all the possible applications.
Color transfer
Michiel Stock (mentioned earlier) showed some a great example in his notes on optimal transport:
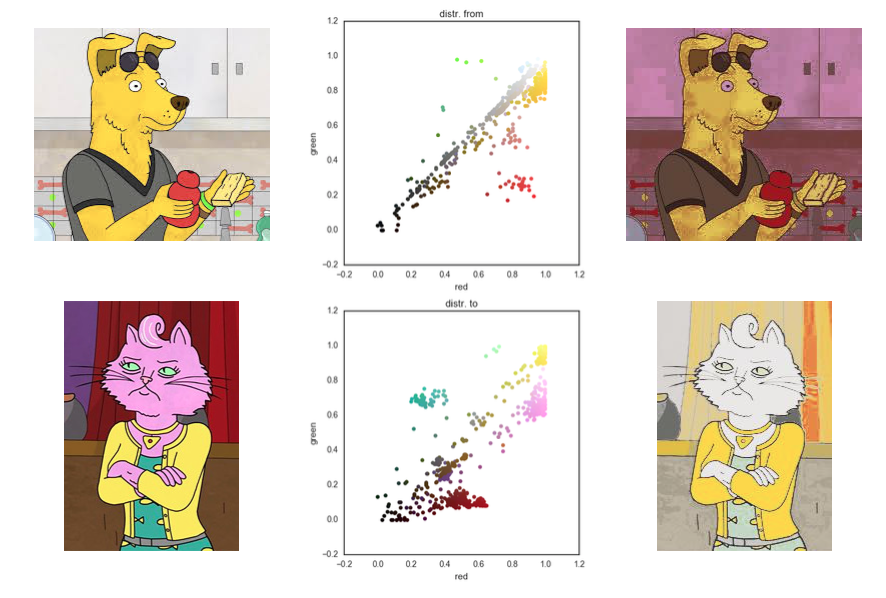
Cool, right? Conceptually, it’s ‘moving’ all those color-palette-histogram points to coincide with color-palette-histogram points from another image.
Two improvements leap to mind:
First, notice how the semantic information like ‘skin color’ doesn’t transfer. We can’t expect the algorithm to know about that. But I bet you could simply encode this as part of the optimization formulation without greatly modifying the algorithm… I.e., simply change the inputs but keep the code mostly intact.
Second, notice the artifacts in the target image on the top-right. It looks like those are JPEG (or video) encoding artifacts from the input image, unintentionally emphasized by the color transfer algorithm. It’d be interesting to apply Michiel’s code to highly-compressed JPEGs and ‘blocky’ images (like Haar wavelet encoded) to see if this is indeed the case.
Michiel kindly shared the source code for this implementation, too.
Here’s another example of color transfer, this time fixing the artifacts with entropy-regularization:
Color transfer using entropy-regularized optimal transport and unregularized optimal transport! pic.twitter.com/GzJy0Ev50l
— Mathieu Blondel (@mblondel_ml) August 25, 2017
Lucky for us, there are several simple open source implementations of OT to experiment with.
The Python Optimal Transport library (POT) includes IPython notebooks that demonstrate color transfer via Ferradans et al. technique:
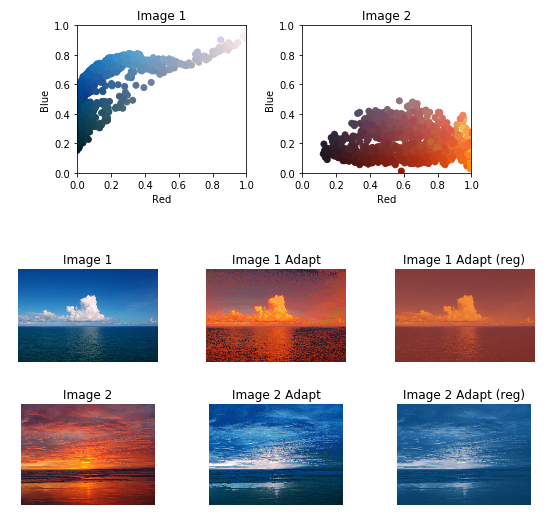
The original images are on the left, color transfer via EMD in the center, and color transfer via Sinkhorn (regularized) on the right.
It’s a pretty amazing result – they’re almost like day for night shots, but in this case they’re “day for sunset” shots!
And another example with mapping estimation:

This result focuses on transforming just the ‘daytime’ source image (top-left), and shows two additional approaches (right column of images): linear mapping estimation, and Gaussian mapping estimation.
Romain Petit’s color transfer IPython notebook show promising results:


Distance metric
We can use optimal transport as a distance metric between ‘objects’. An ‘object’ could be just about anything: an image, a song, a video, a book, et cetera.
That distance metric measures the work required to transform a source object into a target object.
We can apply that metric as a form of similarity, to cluster (un)related items together in an online recommendation system.
This could be applied to find images with similar palettes, for example. It’s something I’m considering for my 3D color palette tool.
Fluid simulation
This image shows how OT can be used to encore incompressibility in fluid simulation:

Interpolating between sounds
Henderson & Solomon 2019 created a method to blend between any two sounds:
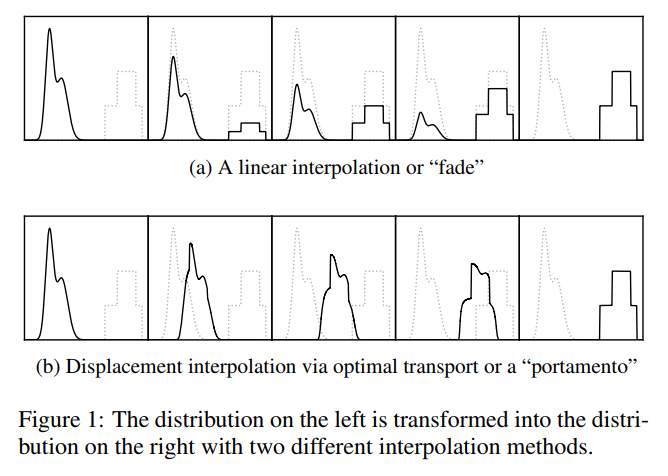
SoundCloud’s embed feature was broken, otherwise I’d just embed the examples here, but here’s a playlist of 7 example sounds generated by this technique. This one is my favorite.
Interpolating 3D meshes
OT can be applied to point in any dimension, which means we can interpolate 3D meshes and volumes:

Resources
Another point-cluster-interpolation demo:
— Alex Mordvintsev (@zzznah) July 10, 2019
After reading Michiel’s intro to OT (linked above), you might like to watch Gabriel Peyre’s talk on applications of OT to computer graphics and AI (slides here).